Progressão Aritmética

A Progressão Aritmética representa uma sequência numérica em que seus componentes são espaçados sempre por um mesmo valor. Considere a sequência abaixo:

(2, 4, 6, 8, 10, 12, …)

Seu primeiro termo é 2. Na nomenclatura matemática, temos que a₁=2. Repare que os termos são espaçados de dois em dois. Portanto, diz-se que a razão da progressão aritmética é dois. Na nomenclatura utilizada, r=2.

A fórmula que indica o somatório de n termos em uma P.A. (progressão aritmética) é a seguinte:

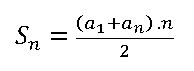
Essa fórmula, inventada (ou descoberta) por Gauss, pode ser assim explicada: A somatória dos n primeiros termos de uma P.A. (S_n) é obtida somando-se o primeiro termo da P.A. com o último termo desejado (a₁ + a_n), multiplicando pelo número de termos da P.A. (n) e dividindo por 2.

Agora, a explicação através da história. Diz-se que Gauss estava na primeira série do primário quando escreveu a fórmula. Sim, do primário! O professor estava cansado do barulho da sala e deu a seguinte tarefa, a ser resolvida individualmente:

– Somem todos os números de 1 a 100!

Em apenas alguns minutos, Gauss chegou com o resultado: 5.050. O professor achou estranho e, conferindo o resultado, viu que estava correto.

Eis a lógica utilizada por Gauss: na sequência dos números de 1 a 100, a soma dos extremos é sempre a mesma: 101. Por exemplo: 1 + 100, 2 + 99, 3 + 98 e assim sucessivamente. Portanto, se pegássemos o resultado dessa soma e multiplicássemos pelo número de vezes em que ela aparece, temos com facilidade um resultado. Essa soma aparece quantas vezes? Cem? Não, pois se percorrermos a sequência inteira, chegaremos ao seguinte ponto: 49 + 52, 50 + 51, 51 + 50, 52 + 49 etc. Repare que começamos a repetir o resultado. Portanto, essa soma está duplicada. Temos que multiplicar 101 pela metade do número total dos termos. Logo, a soma de todos os números de 1 até 100 é igual a 101 vezes 100/2, que é igual a 101 vezes 50, resultando 5.050.

Observe a fórmula novamente:

E sua aplicação neste caso:

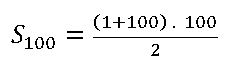
O entendimento da fórmula fica muito mais simples quando entendemos sua história e a lógica por trás do raciocínio.